Berekenen Van Driehoekszijde Met Hoek In Nederlands

Wat is driehoek zijde berekenen met hoek?

Het berekenen van de zijde van een driehoek met een gegeven hoek is een belangrijke vaardigheid in de meetkunde. Deze berekening stelt ons in staat om de lengte van een zijde te vinden wanneer we de mate van een hoek kennen. Dit kan nuttig zijn bij het oplossen van geometrische problemen, het bouwen van structuren of het bepalen van afstanden.

Het berekenen van de zijde van een driehoek met een gegeven hoek kan op verschillende manieren worden gedaan. Het kan worden gedaan met behulp van specifieke formules, zoals de Stelling van Pythagoras of trigonometrische formules zoals de sinus, cosinus en de tangens. We zullen deze methoden later in dit artikel nader bekijken.

Het kennen van de lengte van de zijde van een driehoek met een gegeven hoek stelt ons in staat om de driehoek volledig te begrijpen en andere eigenschappen ervan te bepalen, zoals het berekenen van de oppervlakte, het vinden van ontbrekende hoeken, enzovoort. Dit is waarom het zo belangrijk is om de methoden te begrijpen voor het berekenen van de zijde van een driehoek met een hoek.

Hoe werkt de schuine zijde berekenen met hoek?

Het berekenen van de schuine zijde van een driehoek met een gegeven hoek kan worden gedaan door het toepassen van de Stelling van Pythagoras of door het gebruik van trigonometrische functies zoals de sinus, cosinus en de tangens.

Stelling van Pythagoras: De Stelling van Pythagoras stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de hypotenusa gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden. Dit kan worden geschreven als a^2 + b^2 = c^2, waarbij a en b de lengtes zijn van de rechthoekzijden en c de lengte van de hypotenusa.

Als we de waarde van één zijde van de driehoek en de hoek ertegenover kennen, kunnen we de schuine zijde berekenen met behulp van de Stelling van Pythagoras. We kunnen de lengte van de ontbrekende zijde vinden door de waarde van de bekende zijde in de formule in te voeren en vervolgens de vierkantswortel te nemen om de lengte van de schuine zijde te vinden.

Trigonometrische functies: De sinus, cosinus en tangens van een hoek in een rechthoekige driehoek kunnen worden gebruikt om de lengtes van de zijden te bepalen. De sinus van een hoek is gedefinieerd als de verhouding van de lengte van de overstaande zijde tot de lengte van de hypotenusa. De cosinus van een hoek is gedefinieerd als de verhouding van de lengte van de aanliggende zijde tot de lengte van de hypotenusa. De tangens van een hoek is gedefinieerd als de verhouding van de lengte van de overstaande zijde tot de lengte van de aanliggende zijde.

Om de schuine zijde te berekenen met behulp van de trigonometrische functies, kunnen we de bekende zijde vermenigvuldigen met de verhouding van de lengte van de schuine zijde tot de lengte van de overstaande of aanliggende zijde, afhankelijk van welke zijde bekend is. Deze berekening kan worden uitgevoerd met behulp van een calculator of online tool.

Formule voor het berekenen van de schuine zijde met een hoek van 90 graden

Als we een rechthoekige driehoek hebben met een hoek van 90 graden, kunnen we de schuine zijde eenvoudig berekenen met behulp van de Stelling van Pythagoras. In dit geval worden de lengtes van de zijden van de driehoek gegeven door a^2 + b^2 = c^2, waarbij a en b de lengtes zijn van de rechthoekzijden en c de lengte van de hypotenusa. We kunnen de lengte van de schuine zijde vinden door de kwadraten van de lengtes van de rechthoekzijden op te tellen en vervolgens de vierkantswortel te nemen.

Voorbeeld: Laten we zeggen dat we een rechthoekige driehoek hebben met een lengte van de ene zijde van 3 en een lengte van de andere zijde van 4. We kunnen de lengte van de schuine zijde berekenen door deze waarden in de formule in te voeren:

a^2 + b^2 = c^2
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2

Om de lengte van c te vinden, nemen we de vierkantswortel van beide kanten van de vergelijking:

c = √25
c = 5

Dus de lengte van de schuine zijde is 5.

De sinus, cosinus en tangens gebruiken om de schuine zijde te berekenen

Als we een niet-rechthoekige driehoek hebben met een gegeven hoek en een bekende zijde, kunnen we de sinus, cosinus en tangens gebruiken om de lengte van de schuine zijde te berekenen. Deze trigonometrische functies stellen ons in staat om de verhouding tussen de zijden van de driehoek te bepalen en zo de ontbrekende lengte te vinden.

De sinus van een hoek is gelijk aan de lengte van de overstaande zijde gedeeld door de lengte van de hypotenusa. De cosinus van een hoek is gelijk aan de lengte van de aanliggende zijde gedeeld door de lengte van de hypotenusa. De tangens van een hoek is gelijk aan de lengte van de overstaande zijde gedeeld door de lengte van de aanliggende zijde.

Om de schuine zijde te berekenen met behulp van de sinus, cosinus of tangens, vermenigvuldigen we de lengte van de bekende zijde met de verhouding van de lengte van de schuine zijde tot de lengte van de overstaande of aanliggende zijde, afhankelijk van welke zijde bekend is.

Voorbeeld: Laten we zeggen dat we een driehoek hebben met een hoek van 30 graden en een bekende zijde van 5. We willen de lengte van de schuine zijde berekenen. We kunnen de sinus van 30 graden gebruiken om de verhouding tussen de zijden te bepalen:

sin(30) = overstaande/hypotenusa
sin(30) = overstaande/5

Nu kunnen we de verhouding gebruiken om de overstaande zijde te berekenen:

overstaande = sin(30) * 5

Door deze berekening uit te voeren, krijgen we:

overstaande = 0,5 * 5
overstaande = 2,5

Dus de lengte van de overstaande zijde is 2,5. Nu kunnen we de Stelling van Pythagoras gebruiken om de lengte van de schuine zijde te berekenen.

Toepassing van de Stelling van Pythagoras bij het berekenen van de schuine zijde

De Stelling van Pythagoras is een wiskundige formule die wordt gebruikt om de lengte van een zijde van een rechthoekige driehoek te berekenen. Het stelt dat het kwadraat van de lengte van de hypotenusa gelijk is aan de som van de kwadraten van de lengtes van de andere twee zijden.

Om de schuine zijde van een driehoek te berekenen met behulp van de Stelling van Pythagoras, moeten we weten welke zijden van de driehoek bekend zijn. Als we de lengtes van de rechthoekzijden kennen, kunnen we de lengte van de schuine zijde berekenen door de bekende lengtes in de formule in te voeren en de vierkantswortel te nemen van het resultaat.

Voorbeeld: Laten we zeggen dat we een rechthoekige driehoek hebben met een lengte van de ene zijde van 3 en een lengte van de andere zijde van 4. We kunnen de lengte van de schuine zijde berekenen met behulp van de Stelling van Pythagoras:

a^2 + b^2 = c^2
3^2 + 4^2 = c^2
9 + 16 = c^2
25 = c^2

Om de lengte van c te vinden, nemen we de vierkantswortel van beide kanten van de vergelijking:

c = √25
c = 5

Dus de lengte van de schuine zijde is 5.

Praktische tips en voorbeelden voor het berekenen van de schuine zijde met een hoek

– Zorg ervoor dat de hoek die je gebruikt in graden is. Als de hoek is gegeven in radialen, moet je deze eerst omzetten naar graden voordat je de berekeningen uitvoert.
– Wees voorzichtig bij het gebruik van de juiste trigonometrische functie voor het berekenen van de lengte van de zijden. De sinus wordt gebruikt voor de verhouding van de overstaande zijde tot de hypotenusa, de cosinus voor de verhouding van de aanliggende zijde tot de hypotenusa, en de tangens voor de verhouding van de overstaande zijde tot de aanliggende zijde.
– Gebruik een rekenmachine of online calculator om de berekeningen gemakkelijker uit te voeren en nauwkeurige resultaten te krijgen.
– Oefen met verschillende voorbeelden om je begrip van de concepten te verbeteren en vertrouwd te raken met de stappen die je moet volgen om de schuine zijde te berekenen.

Voorbeeld: Laten we zeggen dat we een driehoek hebben met een hoek van 45 graden en een bekende zijde van 8. We willen de lengte van de schuine zijde berekenen met behulp van de tangens:

tan(45) = overstaande/aanliggend
tan(45) = overstaande/8

Nu kunnen we de verhouding gebruiken om de overstaande zijde te berekenen:

overstaande = tan(45) * 8

Door deze berekening uit te voeren, krijgen we:

overstaande = 1 * 8
overstaande = 8

Dus de lengte van de overstaande zijde is 8. Nu kunnen we de Stelling van Pythagoras gebruiken om de lengte van de schuine zijde te berekenen.

Hulpmiddelen en online calculators voor het gemakkelijk berekenen van de schuine zijde van een driehoek met een hoek

Er zijn verschillende online bronnen en calculators die het gemakkelijk maken om de schuine zijde van een driehoek met een gegeven hoek te berekenen. Hier zijn enkele handige hulpmiddelen die kunnen worden gebruikt:

– Schuine zijde driehoek berekenen – Hypotenusa Calculator: Deze online calculator berekent de lengte van de schuine zijde van een driehoek met behulp van de Stelling van Pythagoras en de gegeven zijden.
– Driehoek berekenen – Bereken de zijden, hoeken, oppervlakte …: Deze website bied

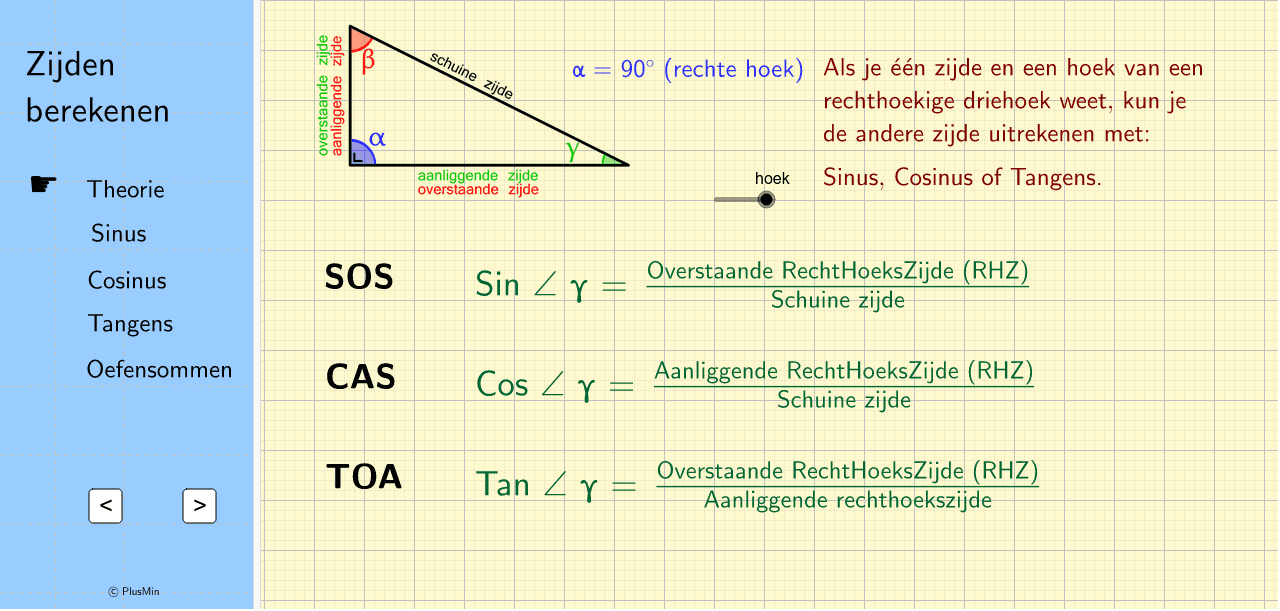
De formule die je kan gebruiken om de schuine en lange zijde van een driehoek te berekenen is c = √(a² + b²). Deze formule werkt alleen met rechthoekige driehoeken met een hoek van 90 graden.De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a² + b² = c². Hierin zijn a en b de rechthoekszijden en c de schuine zijde.Deze noemen we ook wel de hypothenusa. Met de formule sinus = overstaande rechthoekszijde / schuine zijde kunnen we de hoeken en zijden berekenen in een rechthoekige driehoek. De sinus is altijd een verhouding tussen 2 zijden. Met sin^–1 (een knop op je rekenmachine) bepalen we de hoek in graden.

Hoe Bereken Je Een Zijde Van Een Driehoek Uit?

Hoe Bereken Je Een Zijde Als Je Een Hoek En Een Zijde Hebt?

Hoe Bereken Je Zijde Met Hoeken?

Hoe Bereken Je Gelijkzijdige Driehoek?

Hoe Laat Ik Met Een Berekening Zien Dat Een Driehoek Rechthoekig Is?

Top 22 driehoek zijde berekenen met hoek